Web Release Date: February 22,
Copyright © 2001 American Chemical Society
Time-Dependent Reactive Scattering of the H-
+ H2 H2 + H- System
H2 + H- System
Theoretische Chemie, Universität Siegen, D-57068 Siegen, Germany
Received: December 14, 2000
Abstract:
Quantum mechanical calculations of reaction probabilities for the ion-neutral
molecule collisions H- + H2 The above reaction belongs to the family of hydrogen exchange reactions.
In contrast to the neutral reaction H + H2 In recent years, H3- has been investigated rather
intensively experimentally and theoretically. There exist two types of
calculations for the potential energy surface: (a) the ab initio calculations
of the ground-state PES by Stärck and Meyer (SM)6 and (b)
the diatomics-in-molecules (DIM) investigations of Belyaev et al.7-9 This paper is organized as follows: in section II we present the theoretical
approach and in section III we will concentrate on our applications.
B. Formalism. The general theory and various numerical aspects
of time-dependent reactive scattering have been discussed elsewhere.19,33-37 where R is the distance between the atom A and the center of
mass of the BC molecule, {qi} are the internal degrees
of freedom for the BC molecule, and The dynamics of the system is followed by solving the time-dependent
Schrödinger equation for nuclear motion numerically
where with Û being the evolution operator for the Schrödinger
equation and where The Hamiltonian operator in Jacobi coordinates (R, r, with
Here, The wave function for a particular total angular momentum quantum number
J and its space fixed z components can be expressed in terms
of body-fixed coordinates in the form
where M is the quantum number of the projection of total angular
momentum J on the space-fixed z-axis and with the coupling term
The action of terms of type H The propagation of the wave packet can be performed in two different
ways. In the first case we use the Chebyshev propagation method as proposed
by Tal-Ezer and Kosloff.21 The evolution operator is developed
in complex Chebyshev polynomials The Chebyshev polynomials where x = -iHnorm, Alternatively, one can perform one long propagation step as described
by Mandelshtam and Taylor (see eq 3.1 in ref 23):
The absorbing potential is simulated by In eqs 16 and 17, Hs is a scaled and shifted Hamiltonian
operator
where as = 2/ The second method of propagation of the wave packet is the split operator
technique where we approximate the propagator by dividing the total time
into N segments To get an overview about other ways of performing the action of the
propagator the reader is referred to the literature.40,41
In both schemes (CH, SO) the action of the radial kinetic energy on
the wave function is used in conjunction with the fast Fourier method (FFT);
in case of angular kinetic energies a discrete variable representation
method is used (DVR). The kinetic and potential energy is given as follows.
Radial kinetic energy for the R coordinate (and for r, respectively)
is (a) for Chebyshev:
where k is the wave vector of a given plane wave. For (b) for
SO:
The angular kinetic energy (angle with
and for (b) SO:
with (1/I) = ((1/ Although the last two formulations (eqs 23 and 25) seem to be clear
with respect to numerical implementation, there have been some complications
if not enough memory is available within the program code. In the case
of Chebyshev implementation, the moment of inertia Iil
is indexed with respect to Ri and
rl
values. If one defines a maximum energy value for the angular kinetic energy
contribution, it might be possible to define a jmax =
f(Emax) value for the case that the prefactor
(1/2I) does not become too large. In that case, one can save computation
time by storing a new matrix Ukk'
in which (1/2I) has been separated out. In case of large (1/2Iil)
values (i.e., for R otherwise the transformation given in eq 25 becomes the most time-consuming
step during the propagation, although H The potential energy is diagonal in the coordinate grid representation,
and the action in the CH approach is just a multiplication
whereas in the SO approach, the wave function has to be multiplied twice
with the e-iV(Rirl, As mentioned before, the wave function is discretized on a 3D grid in
Jacobi coordinates R, r, and C. Analysis. In our calculations we can perform energy-resolved
state-to-state and flux calculations. The wave packet is propagated until
it has "completely" left the interaction region. To perform the analysis
we need the wave packet in the correct Jacobi coordinates, depending on
the different possible arrangement channels Because of that reason, we perform for each reactive product arrangement
channel an individual scattering calculation performed in the appropriate
product Jacobi coordinates as illustrated in Figures 1 and 2. If only global
reaction probabilities are needed, one can calculate within the reactant
Jacobi coordinates the state-to-state inelastic transition probabilities
and calculate the reaction probabilities as the difference from unity:
The disadvantage of propagating in product coordinates is that the representation
of the starting wave packet needs more angular grid points for an appropriate
description with a given quality of the norm of the wave function. The
analysis for the reaction probability or the S-matrix can be performed
in two ways: (a) we can split off the wave packet in the asymptotic region
(as proposed by Heather and Metiu24) or (b) calculate the contribution
at an asymptotic analysis line as proposed by Balint-Kurti et al.27
In case of splitting off the wave function Rp and C define the shape of the split-off
function. After each time step, the product part is split off and the interaction
part is analyzed. Its contribution to the S-matrix is given by
After each splitting, the propagation is continued, with (1 -
f) In the Balint-Kurti-approach,27 the S-matrix is calculated
by the following procedure: in the asymptotic region, i.e., R is
large, first the wave packet along a cut (Rana) is projected
onto the final product state Then these coefficients are Fourier transformed over the time to give
energy dependent coefficients AF,I(E)
and the S-matrix results from the simple relation (derivation given
in refs 38 and 39):
If just energy resolved reaction probabilities where in case of reactant Jacobi coordinates the quantity in the brackets
is the energy-resolved flux of the wave packet at the asymptotic dividing
surfaces defined at the position rana (for reactive analysis)
or at Rana (for inelastic analysis); the angular brackets
denote integration over the other two coordinates. The energy-dependent
wave function To avoid unphysical reflections of the wave function arising from finite
size boundary of the coordinate grid (this is needed at least for the asymptotic
analysis procedures at asymptotic cut-lines of flux calculations through
a dividing surface), the outer part of the radial part of the grid is surrounded
by an optical (absorbing) potential of the form proposed by Vibok and Balint-Kurti;32
we mostly use the type given in eq 18.
To summarize our approach: there are two ways for a state selective
analysis: (1) Figure 2a: For inelastic 3D-investigations we use reactant
Jacobi coordinates, so that a state-to-state inelastic analysis is possible
and energy resolved total reaction probabilities can be calculated. (2)
Figure 2b: In case of reactive 3D-investigations we use product Jacobi
coordinates, so that state-to-state reaction probabilities can be calculated.
The advantage is that no coordinate transformation of the wave packet
is necessary. The transformation of the wave packet, from one coordinate
system (e.g., reactant coordinates) to the one that is optimal for asymptotic
analysis (e.g., product coordinates) is time-consuming and leads to numerical
inaccuracies.
For most of the calculations in this present work, the width of the
wave packet is chosen such that within one WP calculation accurate results
for a collision energy range of ± 1 to 2 eV around the initial starting
collision energy can be achieved. The quality of the propagation depends,
for a given collision energy, on the propagation time length and all internal
parameters, such as grid size for the coordinates, width of the wave packet,
etc. We accept a propagation as being reasonable if the contributions coming
from the rana and Rana analysis line
add up to 100 ± 1-3%. This test has been performed by adding up
(a) fluxes through the rana and Rana
intersection line, (b) adding up flux through the rana
and state-to-state contributions calculated at the Rana
intersection line (or vice versa), or (c) adding up from two individual
runs the state-to-state contributions calculated at the Rana
intersection line for reactant and product Jacobi coordinates.
Reaction a will be discussed in the present paper, reactions b and c
in a forthcoming paper.51 The H3- system
is of great importance in hydrogen plasmas.18 We are using the
potential energy surface of Stärck and Meyer6 and the diatomics-in-molecules
(DIM) potential of Belyaev.7 A comparison of scattering calculations
with the experiment will be a test for the quality of DIM surfaces, which
nowadays are often used for reactive dynamics, especially on coupled surfaces.
In case of inelastic investigations for H3- at high
energies (up to keV), the DIM results had been reasonable compared to experiment.14
The 3D DIM PES for the ground state and some low lying excited states
was reported by Belyaev et al.8,9 Ground and first excited state
form a conical intersection at D3h symmetry. The
ab initio surface of Stärck and Meyer6 has been determined
by MR-CI and CEPA(2) calculations for 403 nuclear configurations. It has
been cast in an analytical form by a fit with 23 parameters and an rms
error of 0.23 mEh. The PES fit presented in ref 6 includes
some misprints, so we were happy that W. Meyer could provide us with his
code for the PES. This code had been tested by using quasiclassical trajectory
calculations,52 and no numerical problems from the fit were
encountered. Within our WP calculations we found that in a small region
in the strong repulsive part of the potential, i.e., at short H-H-distances,
the energy tends to go to minus infinity (this results from eq 1 in ref
6). We corrected this behavior, so that the only minimum region on the
global surface is the linear van der Waals minimum in the entrance channel
(r = 1.416a0, R = 6.183a0, Because of the existence of several electronic excited states at energies
E > 1.2 eV, a nuclear dynamics calculation involving several electronic
states is necessary for E > 1.2 eV. In this paper we will present
calculations on a single surface, which should be reasonable at least up
to E = 1.2 eV. The influence of higher excited states on the dynamics
has to be investigated in the future. Collinear reactions have been investigated
in recent years using both the DIM and the SM potential. Inelastic scattering
calculations for higher collision energies has been reported by Gianturco
and Kumar.13 The first energy resolved reaction probabilities
in three dimensions on the DIM PES using the time-dependent WP approach
has been presented by Mahapatra;15 some preliminary calculations
using the SM PES have been reported by Mahapatra and Sathymurthy.16
In this paper we will concentrate mostly on time-dependent WP calculations
using the SM potential, because, as will be seen in the next subsections,
the DIM PES leads to very different results concerning the reaction probabilities.
To check our own code and to compare with time-independent approaches,
we performed in addition calculations using the hyperspherical coordinate
method of Manolopoulos et al.54
The numerical grid parameters and properties of the initial wave function
used in the calculations of total and state-to-state reaction probabilities
are summarized in Table 1.
B. H- + H2. In the following three figures
(Figures 3, 4, and 5) Within Figures 3-5 we compare different wave packet approaches (different
coordinates, propagators, etc.). In principle the results are qualitatively
the same (in order not to overload the figures, not every result is shown),
but if one is interested in very accurate, detailed information, the Chebychev
method is clearly the one to be preferred. To get a rough overview of the
reaction probability, the split-operator approach performs better, compared
to the Chebychev method (this results from fewer actions of the Hamiltonian
within the propagation). For the H3- system we find
only few resonances, which are smoothed a bit when using the split-operator
approach (presumably the time step The work of Mahapatra and Sathyamurthy16 performed with the
SM potential shows much more pronounced resonances, which we attach especially
to a too early starting position for the wave packet, the use of the SO
method, and a smaller number of grid points. In the work of Mahapatra15
using the DIM potential, most of these ingredients have been improved,
but the DIM potential is less demanding with respect to resonances, except
for H- + H2 (v = 2), where some resonance
features are seen in the onset of the reaction probability. On the other
hand, we see strong resonance features for all initial H2 (v
> 0), but one has to keep in mind that most of these features do happen
at energies above the opening of the detachment channel.
In Figure 8 (a smaller energy section is seen in Figure 9), we test
the influence of increasing the range of the interaction potential. The
maximum value for R has been chosen between 15.5 and 19.5a0.
Results presented in Figures 3-5 have been calculated for Rmax
= 15.5a0, and the new results presented in Figure 8 reveal
that Rmax was too short, because the reaction probability
around E = 0.9 eV is too low. In addition, we compare (a) our code
for complex wave packets, (b) the real wave packet code of Stephen Gray,53
and (c) the time-independent "ABC"-code of Manolopoulos et al.;54
for the three different codes all calculations have been performed by ourselves.
The results for the complex and real wave packets are nearly identical
if the same numerical parameters have been used (Figure 9). There is a
slight difference in the results when we compare WPs with different initial
starting collision energies (Figure 9: Etrans = 1 eV,
2 eV). If the hyperspherical radius In the next figures (Figures 10, 11, 12, 13), we present results for
state-to-state reaction probabilities. If one starts initially with
v
= 0, j = 0, then for the product molecule mainly vibrational state
v = 0 is preferred (Figure 10), whereas in case of the final product
H2 (v = 0), especially the rotational states j
= 1 and j = 0 (Figure 11) dominate; similar results are seen for
for final vibrational v = 1 (Figure 12) and v = 2 states
(Figure 13).
In Figure 14, we present results for the total reactive cross section
using the J-shifting method of Bowman et al.48-50 Part of our project is to clarify, which numerical technique is the
most efficient for solving wave packet propagation, especially when using
the code on multiprocessor machines. For the present applications, we can
say that the Chebychev method is clearly the one to be preferred, because
the accuracy can be improved by propagating in time as long it is needed.
The recursion formula in eq 16 is independent of the magnitude of the time
step. If high accuracy is preferred, the split-operator method needs time-steps
of The advantages of wave packet (WP) calculations are that WPs are relatively
easy to apply for systems with many reaction channels, that WPs are suitable
for the use on several PESs, and that with WPs one gets, within one calculation,
information about a large collision energy range ( In the case of the H3- system, we presented energy-resolved
and state-to-state reaction probabilities for different starting conditions.
It is for the first time that the nuclear dynamics within the H3-
system has been investigated in such a detail using mostly the ab initio
potential of Stärck and Meyer (SM)6 and that the results
have been checked by us with two other time-dependent and time-independent
approaches. We calculated reaction probabilities for the DIM and ab initio
PES: the results are qualitatively different.
We could show that our results are quantitatively comparable with the
real wave packet code of S. Gray53 and with the "ABC" code (time-independent
hyperspherical coordinate method) of Manolopoulos et al.54 A
direct comparison between theory and experiment can be made when our integral
and differential cross sections are available. We are in the process of
finishing this work. Most of the experimental work for reactive analysis
is performed for the isotopic variants HD2- and DH2-;
our results for these systems will be soon available. We are planning now
to perform the WP calculations on several surfaces, initially using the
DIM approach.
* Corresponding author, ralph.jaquet@theo.chemie.uni-siegen.de.
1. State-Selected and State-to-State Ion-Molecule Reaction Dynamics:
Experiment and Theory in Advances in Chemical Physics; Baer, M.,
Ng, C. Y., Eds.; Wiley: New York, 1992; Vol. 81, 82.
2. Cencek, W.; Rychlewski, J.; Jaquet, R.; Kutzelnigg, W. J. Chem.
Phys. 1998, 108, 2831; 3. Röhse, R.; Kutzelnigg, W.; Jaquet, R.; Klopper, W. J. Chem.
Phys.1994, 101, 2231. 4. Pendergast, P.; Heck, J. M.; Hayes, E. F.; Jaquet, R. J. Chem.
Phys.1993, 98, 4543. 5. Jaquet, R. J. Theor. Chim. Acta 1994, 88, 217. 6. Stärck, J.; Meyer, W. Chem. Phys. 1993, 176,
83. 7. Belyaev, A. K.; Colbert, D. T.; Groenenboom, G. C.; Miller, W. H.
Chem. Phys. Lett. 1993, 209, 309. 8. Belyaev, A. K.; Tiukanov, A. S. Chem. Phys. 1997, 220,
43. 9. Belyaev, A. K.; Tiukanov, A. S. Chem. Phys. Lett. 1999,
302, 65. 10. Miller, W. H.; Hansen op de Harr, B. M. D. D. J. Chem. Phys.
1987, 86, 6213. 11. Zhang, J. Z. H.; Chu, S. I.; Miller, W. H. J. Chem. Phys.
1988, 88, 6233. 12. Miller, W. H. In Advances in Molecular Vibrations and Collision
Dynamics; Bowman, J. M.; Ed.; JAI Press: Greenwich, CT, 1994; Vol.
2A, p 1.
13. Gianturco, F. A.; Kumar, S. J. Chem. Phys. 1995, 103,
2940; 14. Gianturco, F. A.; Kumar, S. J. Phys. B: At. Mol. Opt. Phys.
1997,
30, 3031. 15. Mahapatra, S. Phys. Chem. Chem. Phys. 2000, 2,
671. 16. Mahapatra, S.; Sathyamurthy, N. Faraday Discuss. 1998,
110, 228. 17. Haufler, E.; Schlemmer, S.; Gerlich, D. J. Phys. Chem. A
1997,
101, 6441. 18. Zimmer, M.; Linder, F. J. Phys. B: At. Mol. Opt. Phys.
1995, 28, 2671. 19. Kosloff, R. J. Phys. Chem. 1988, 92, 2087. 20. Goldfield, E. M.; Gray, S. K. Comput. Phys. Commun. 1996,
98, 1. 21. Tal-Ezer, H.; Kosloff, R. J. Chem. Phys. 1984, 81,
3967. 22. Feit, M. D.; Fleck, J., Jr.; Steiger, A. J. Comp. Phys. 1982,
47, 412. 23. Mandelshtam, V.; Taylor, H. S. J. Chem. Phys. 1995,
103, 2903. 24. Heather, R.; Metiu, H. J. Chem. Phys. 1987, 86,
5009. 25. Neuhauser, D.; Baer, M.; Hudson, R. S.; Kouri, D. J. Comput.
Phys. Commun. 1991, 63, 460. 26. Leforestier, C. J. Chem. Phys. 1991, 94, 6388. 27. Balint-Kurti, G. G.; Dixon, R. N.; Marston, C. C. Int. Rev. Phys.
Chem. 1992, 11, 317. 28. Brigham, E. O. The Fast Fourier Transformation: An Introduction
to its Theory and Application; Prentice Hall: New Jersey, 1974.
29. Light, J. C.; Hamilton, I. P.; Lill, J. V. J. Chem. Phys.
1985, 82, 1400. 30. Gray, S. K.; Balint-Kurti, G. G. J. Chem. Phys. 1998,
108, 950. 31. Meijer, A. J. H. M.; Goldfield, E. M.; Gray, S. K.; Balint-Kurti,
G. G. Chem. Phys. Lett. 1998, 293, 270. 32. Vibok, A.; Balint-Kurti, G. G. J. Phys. Chem. 1992,
96, 8712. 33. Kulander, K. C.; Ed.; Time-Dependent Methods for Quantum Dynamics,
Comput. Phys. 1991, 63; Special Issue.
34. Cerjan, C., Ed.; Numerical Grid Methods and their Application
to Schrödinger's Equation; NATO ASI Series C 412; Kluwer: Dordrecht,
1993.
35. Balakrishnan, N.; Kalyanaraman, C.; Sathyamurthy, N. Phys. Rev.1997,
280, 79. 36. Wyatt, R. E.; Zang, J. Z. H., Eds.; Dynamics of Molecules and
Chemical Reactions; Marcel Dekker: New York, 1996.
37. Manz, J. In Femtochemistry and Femtobiology-Ultrafast reaction
dynamics; Sundström, V., Ed.; World Scientific: Singapore, 1997.
38. Balint-Kurti, G. G.; Dixon, R. N.; Marston, C. C. J. Chem. Soc.,
Faraday Trans. 1990, 86, 1741. 39. Offer, A. R.; Balint-Kurti, G. G. J. Chem. Phys. 1994,
101, 10416. 40. Leforestier, C.; Bisseling, R. H.; Cerjan, C.; Feit, M. D.; Friesner,
R.; Guldenberg, A.; Hammerich, A.; Jolicard, G.; Karrlein, W.; Meyer, H.
D.; Lipkin, N.; Roncero, O.; Kosloff, R. J. Comp. Phys. 1991,
94, 59. 41. Truong, T. N.; Tanner, J. J.; Bala, P.; McCammon, J. A.; Kouri,
D. J.; Lesyng, B.; Hoffman, D. K. J. Chem. Phys. 1992, 96,
2077. 42. Zhu, W.; Peng, T.; Zhang, J. Z. H. J. Chem. Phys. 1997,
106, 1742. 43. Kouri, D. J.; Hoffman, D. K.; Peng, T.; Zhang, J. Z. H. Chem.
Phys. Lett. 1996, 262, 519. 44. Althorpe, S. C.; Kouri, D. J.; Hoffman, D. K. J. Chem. Phys.
1997,
107, 7816; 45. Althorpe, S. C. Faraday Discuss. 1999, 110,
238; 46. Jaquet, R.; Kumpf, A.; Heinen, M. J. Chem. Soc., Faraday Trans.1997,
93, 1027. 47. Siegbahn, P.; Liu, B. J. Chem. Phys. 1978, 68,
2547. 48. Bowman, J. M. Adv. Chem. Phys. 1985, 61, 115. 49. Bowman, J. M. J. Chem. Phys. 1991, 95, 4960. 50. Sun, Q.; Bowman, J. M.; Schatz, G. C.; Connor, J. N. L. J. Chem.
Phys. 1990, 92, 1677. 51. Jaquet, R.; to be published.
52. Meyer, W.; private communication.
53. Real wave packet code of S. Gray. See ref 30.
54. Skouteris, D.; Castillo J. F.; Manolopoulos, D. E.; ABC: The
CCP6 Quantum Reactive Scattering Program. Comput. Phys. Comun.
2000, 133, 128. 55. Wave packet calculations for Ne+H2+, to be
published.
 H2 + H- are performed by means of time-dependent
wave packet propagation. Results for two different potential energy surfaces
(ab initio and diatomics-in-molecules) are compared. The calculated state-to-state
reaction probabilities using product-Jacobi-coordinates are compared with
energy resolved reaction probabilities calculated with the flux-operator
using reactant-Jacobi-coordinates and with time-independent calculations.
The shallow potential well of ca. 0.05 eV leads to some resonances in the
reaction probabilities. In addition, we present results for integral cross
sections using the J-shifting method.
H2 + H- are performed by means of time-dependent
wave packet propagation. Results for two different potential energy surfaces
(ab initio and diatomics-in-molecules) are compared. The calculated state-to-state
reaction probabilities using product-Jacobi-coordinates are compared with
energy resolved reaction probabilities calculated with the flux-operator
using reactant-Jacobi-coordinates and with time-independent calculations.
The shallow potential well of ca. 0.05 eV leads to some resonances in the
reaction probabilities. In addition, we present results for integral cross
sections using the J-shifting method.
I. Introduction
In the present project we investigate reactions of the type A + BC (A =
Ne, H(D); B,C = H(D)), where one collision partner is ionic (negative or
positive).1 For the systems H+
+ H22,3

 ).
One of our recent systems is the H- + H2
).
One of our recent systems is the H- + H2 H2 + H- reaction, which we investigate with different
isotope substitutions: H- + H2
H2 + H- reaction, which we investigate with different
isotope substitutions: H- + H2 H2 + H- (R1), H- + D2
H2 + H- (R1), H- + D2 D- + HD (R2), and D- + H2
D- + HD (R2), and D- + H2 H- + HD (R3). In our first investigations we start with calculations
using a single potential energy surface, although it is likely that at
higher energies (E > 1.2 eV) excited electronic states of H3-
might influence the ground-state reaction.
H- + HD (R3). In our first investigations we start with calculations
using a single potential energy surface, although it is likely that at
higher energies (E > 1.2 eV) excited electronic states of H3-
might influence the ground-state reaction.
 H2 + H it has a shallow potential well in the entrance channel,
but the reaction barrier in the interaction region is of comparable magnitude.
Compared to the positively charged system H+ + H2
H2 + H it has a shallow potential well in the entrance channel,
but the reaction barrier in the interaction region is of comparable magnitude.
Compared to the positively charged system H+ + H2 H2 + H+ with a deep minimum of 4.61 eV for the equilibrium
structure of H3+, the well depth of 0.05 eV is relatively
small. What distinguishes ionic systems from neutral systems is that because
of the long-range inductive interaction potential (V ~ -1/R4)
the important range of the PES is much more extended (at least for our
systems: R (atom-diatom)> 16 a0) than in case
of neutral systems.
H2 + H+ with a deep minimum of 4.61 eV for the equilibrium
structure of H3+, the well depth of 0.05 eV is relatively
small. What distinguishes ionic systems from neutral systems is that because
of the long-range inductive interaction potential (V ~ -1/R4)
the important range of the PES is much more extended (at least for our
systems: R (atom-diatom)> 16 a0) than in case
of neutral systems.
II. Quantum Dynamics
A. Introduction. The time-dependent Schrödinger equation is
solved using Jacobi coordinates (see Figure 1) by propagating wave packets
with the Chebychev (CH)19,21
and/or the split-operator method (SO).22 In the case of the
Chebychev method, we test the recursions of (a) Kosloff19 and
(b) Mandelshtam and Taylor.23 Within the wave packet (WP) method,
the wave function is discretized on a grid.19,24-27 0, including the full Coriolis coupling. Within a parallel implementation
(for IBM-SP2) we test different schemes for propagations, kinetic energy
representations and absorbing potentials; this work is in progress.
0, including the full Coriolis coupling. Within a parallel implementation
(for IBM-SP2) we test different schemes for propagations, kinetic energy
representations and absorbing potentials; this work is in progress.


 (q)
is the initial state of the BC molecule for given vibrational (v)
and rotational (j) quantum number. R0, k0,
and
(q)
is the initial state of the BC molecule for given vibrational (v)
and rotational (j) quantum number. R0, k0,
and  define the initial location of
the center of the wave packet in coordinate and momentum space and the
initial width.
define the initial location of
the center of the wave packet in coordinate and momentum space and the
initial width.

 is used as an index for the
different arrangements (
is used as an index for the
different arrangements ( = A + BC,
= A + BC,  = AB + C,
= AB + C,  = AC + B), and the formal
solution is given by
= AC + B), and the formal
solution is given by

 (t = 0) and
(t = 0) and  (t)
are the wave function of the system at time 0 and t, respectively.
(t)
are the wave function of the system at time 0 and t, respectively.
 )
for the body-fixed frame (
)
for the body-fixed frame ( = 1) is given as
= 1) is given as


 R is the reduced mass
of the A - BC system,
R is the reduced mass
of the A - BC system,  r is the
reduced mass of the BC (diatom) molecule, J is the total angular
momentum of the system, j is the rotational angular momentum for
BC, V(R, r,
r is the
reduced mass of the BC (diatom) molecule, J is the total angular
momentum of the system, j is the rotational angular momentum for
BC, V(R, r,  )
is the potential energy surface and J±, j±
are usual ladder operators.
)
is the potential energy surface and J±, j±
are usual ladder operators.


 is the quantum number for the projection of j
is the quantum number for the projection of j on the body-fixed
z-axis.
on the body-fixed
z-axis.  denotes the Wigner rotation matrix elements. The resulting Hamiltonian
in the body-fixed frame is given in a tridiagonal matrix representation,
where, according to eq 5, the diagonal part is of the form
denotes the Wigner rotation matrix elements. The resulting Hamiltonian
in the body-fixed frame is given in a tridiagonal matrix representation,
where, according to eq 5, the diagonal part is of the form


 and H
and H ,± on the
wave function can be computed independently and is optimal for a parallel
implementation.20
,± on the
wave function can be computed independently and is optimal for a parallel
implementation.20
 n
n





 n
are calculated with a recursion formula
n
are calculated with a recursion formula

 0
=
0
=  (0),
(0),  1
= x
1
= x (0).
(0).


 (R,r):
(R,r):


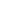 E,
bs = 1 - asEmax as
defined in the equivalent recursion formula by Gray and Balint-Kurti (see
eq 12 in ref 30), which can be used for the complex wave packet (as we
do it in the present paper) or its real part only.30 The recursion
relation can be used to create the complex wave function for a given time
(information from eq 16 has to be inserted into the e(-i
E,
bs = 1 - asEmax as
defined in the equivalent recursion formula by Gray and Balint-Kurti (see
eq 12 in ref 30), which can be used for the complex wave packet (as we
do it in the present paper) or its real part only.30 The recursion
relation can be used to create the complex wave function for a given time
(information from eq 16 has to be inserted into the e(-i t/
t/ )
expansion) or is used as a dynamical iteration alone as in the Gray-Balint-Kurti-approach.
In our implementation we use the various schemes as described above. For
the final analysis we store, in the case of one long propagation, information
from each iteration step; within a test-run one can clarify if for each
iteration the information has to be stored. Details are given in the work
of Gray, Balint-Kurti, and coworkers.30,31
)
expansion) or is used as a dynamical iteration alone as in the Gray-Balint-Kurti-approach.
In our implementation we use the various schemes as described above. For
the final analysis we store, in the case of one long propagation, information
from each iteration step; within a test-run one can clarify if for each
iteration the information has to be stored. Details are given in the work
of Gray, Balint-Kurti, and coworkers.30,31
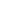 t using
the Trotter formalism of second order. Each short time propagator e-iH
t using
the Trotter formalism of second order. Each short time propagator e-iH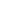 t/
t/ is again splitted symmetrically in the following way (potential referenced
expression)
is again splitted symmetrically in the following way (potential referenced
expression)



 coordinate) for (a) Chebyshev is
coordinate) for (a) Chebyshev is



 RR2)
+ (1/
RR2)
+ (1/ rr2)).
rr2)).

 0) several of these matrices
have to be stored. We have in our program defined an Emax
value which leads to individual jmax values for given
i and l; we think that this is more accurate in the numerical
implementation than a global definition of jmax.
In the case of SO calculations, this trick of separation of (1/2I)
is not possible. If enough core memory is available, one can store
0) several of these matrices
have to be stored. We have in our program defined an Emax
value which leads to individual jmax values for given
i and l; we think that this is more accurate in the numerical
implementation than a global definition of jmax.
In the case of SO calculations, this trick of separation of (1/2I)
is not possible. If enough core memory is available, one can store

 is not as often performed as in the case of Chebyshev propagation.
is not as often performed as in the case of Chebyshev propagation.

 k)
k)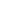 t/2
t/2 factor. In the moment, we use the SO approach only in case of diagonal
potential energy representation.
factor. In the moment, we use the SO approach only in case of diagonal
potential energy representation.
 with typically NR = 64-128, Nr = 64-128,
and N
with typically NR = 64-128, Nr = 64-128,
and N = 32-80 grid points. Ionic
systems require a finer discretization, because deep potentials (typically
Vmin
= 32-80 grid points. Ionic
systems require a finer discretization, because deep potentials (typically
Vmin -0.5
-0.5  -4.5 eV) lead to strong resonances. The propagation time is set (a) by
using N segments of
-4.5 eV) lead to strong resonances. The propagation time is set (a) by
using N segments of 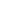 t
in the split operator formalism, (b) by setting a maximum propagation time
and by that fixing the number of N Chebychev iterations for the
propagation as proposed by Kosloff, or (c) by doing one long propagation
step as proposed by Mandelshtam and Taylor and fixing for that the number
of Chebychev iterations. Of course, after the propagation is performed
for a given number of steps, the run can be restarted if the reaction probabilities
do not seem to be converged.
t
in the split operator formalism, (b) by setting a maximum propagation time
and by that fixing the number of N Chebychev iterations for the
propagation as proposed by Kosloff, or (c) by doing one long propagation
step as proposed by Mandelshtam and Taylor and fixing for that the number
of Chebychev iterations. Of course, after the propagation is performed
for a given number of steps, the run can be restarted if the reaction probabilities
do not seem to be converged.
 .
A basic difficulty in the theory of reactive collisions is that the coordinates
appropriate for reactant and product arrangements differ from each other.
There have been different ways presented in the literature to solve the
problem:42-45
.
A basic difficulty in the theory of reactive collisions is that the coordinates
appropriate for reactant and product arrangements differ from each other.
There have been different ways presented in the literature to solve the
problem:42-45
 ,
,  is divided in two parts, the product part
is divided in two parts, the product part  P
and the interaction part
P
and the interaction part  I
as given in eqs 30 and 31:
I
as given in eqs 30 and 31:





 replacing
replacing  . This procedure has the quality
of an absorbing potential so that the wave packet does not reach the end
of the grid point area; otherwise, this leads to numerical problems in
the FFT approach. In case of split-off functions, no further absorbing
potential is needed in the calculation.
. This procedure has the quality
of an absorbing potential so that the wave packet does not reach the end
of the grid point area; otherwise, this leads to numerical problems in
the FFT approach. In case of split-off functions, no further absorbing
potential is needed in the calculation.
 F(r)
to produce a set of time-dependent coefficients CF,I(t)
(e.g., using product Jacobi coordinates):
F(r)
to produce a set of time-dependent coefficients CF,I(t)
(e.g., using product Jacobi coordinates):



 (E)
are desired,
(E)
are desired,  (E) is computed
from (e.g., using reactant Jacobi coordinates)
(E) is computed
from (e.g., using reactant Jacobi coordinates)


 (R, r,
(R, r,  ,
E) is obtained by Fourier transforming
,
E) is obtained by Fourier transforming  (R,
r,
(R,
r,  , t). The described
formulation of the Balint-Kurti analysis approach is straightforward if
using the wave function as given in eq 11 using the recursion relation
in eq 15. In case of using the recursion formula given in eq 16, one has
to take into account that the energy scale was shifted and scaled (see
ref 30; for flux analysis: see ref 31).
, t). The described
formulation of the Balint-Kurti analysis approach is straightforward if
using the wave function as given in eq 11 using the recursion relation
in eq 15. In case of using the recursion formula given in eq 16, one has
to take into account that the energy scale was shifted and scaled (see
ref 30; for flux analysis: see ref 31).
III. Results and Discussion
A. Introduction. The following reactions are currently under investigation
in our group:



 = -0.0476 eV). The position and height of the barrier have been found at
rbar = 1.997a0 and
= -0.0476 eV). The position and height of the barrier have been found at
rbar = 1.997a0 and  = 0.454 eV. The electron detachment seam has been determined and its lowest
point was found for R = 2.86a0, r = 1.42a0,
and
= 0.454 eV. The electron detachment seam has been determined and its lowest
point was found for R = 2.86a0, r = 1.42a0,
and  = 90
= 90 with
an energy of 1.2 eV, which agrees experimental findings.18 The
barrier height of the DIM potential (at the position rHH
= 1.74a0) is by 0.17 eV (
with
an energy of 1.2 eV, which agrees experimental findings.18 The
barrier height of the DIM potential (at the position rHH
= 1.74a0) is by 0.17 eV ( = 0.624 eV) larger than the one of the SM potential. The DIM potential
also exhibits a shallow van der Waals minimum in the entrance channel (
= 0.624 eV) larger than the one of the SM potential. The DIM potential
also exhibits a shallow van der Waals minimum in the entrance channel (
 -0.05 eV) and has a energy threshold value of 1.46 eV for electron detachment.
-0.05 eV) and has a energy threshold value of 1.46 eV for electron detachment.
 ,
we present results of energy-resolved total reaction probabilities of H-
+ H2(v,j) for different intial vibrational (v)
and rotational (j) states. In Figures 3 and 5 we show in addition
the results for the neutral reaction H+H2 using the LSTH potential47
and compare the two potentials SM and DIM. For the SM potential, the reaction
starts at a total energy of E
,
we present results of energy-resolved total reaction probabilities of H-
+ H2(v,j) for different intial vibrational (v)
and rotational (j) states. In Figures 3 and 5 we show in addition
the results for the neutral reaction H+H2 using the LSTH potential47
and compare the two potentials SM and DIM. For the SM potential, the reaction
starts at a total energy of E  0.55 eV (Etrans
= 0.46 eV), similar to the neutral reaction H+H2. Because the
barrier height is larger in case of the DIM potential, there the reaction
starts
0.55 eV (Etrans
= 0.46 eV), similar to the neutral reaction H+H2. Because the
barrier height is larger in case of the DIM potential, there the reaction
starts  0.17 eV later. The forms of the onset of
the reaction probability are completely different if one compares SM and
DIM. In case of the SM potential, the reaction probability for initial
H- +H2 (v = 0, j = 0) (Figure 3) increases
steeply up to 70-80% and falls down slowly around 1.8 eV, whereas for DIM
the reaction probability reaches its maximum for E > 2 eV. For the
SM potential, the reaction probability is a relatively smooth curve comparable
with the neutral H+H2 reaction, except that resonances occur
in some smaller energy ranges for E > 1.2 eV. If one compares Figures
3 (with initial H2 (v = 0, j = 0)) and 4 (with
initial H2 (v = 1, j = 0)), one will see that
for H- + H2 (v = 1, j = 0) the resonance
structure is much more pronounced between E = 1.2 to 1.3 and E
= 1.6 to 1.8 eV. Figure 5 includes results for the different starting conditions
for H2 in different vibrational (v = 0, 1,...) and rotational
states (j = 0, 1,...). The most impressive feature is that for H2
(v = 0, j = 1) the reaction probability increases steeply
up to 95% with some small resonance features around
E
0.17 eV later. The forms of the onset of
the reaction probability are completely different if one compares SM and
DIM. In case of the SM potential, the reaction probability for initial
H- +H2 (v = 0, j = 0) (Figure 3) increases
steeply up to 70-80% and falls down slowly around 1.8 eV, whereas for DIM
the reaction probability reaches its maximum for E > 2 eV. For the
SM potential, the reaction probability is a relatively smooth curve comparable
with the neutral H+H2 reaction, except that resonances occur
in some smaller energy ranges for E > 1.2 eV. If one compares Figures
3 (with initial H2 (v = 0, j = 0)) and 4 (with
initial H2 (v = 1, j = 0)), one will see that
for H- + H2 (v = 1, j = 0) the resonance
structure is much more pronounced between E = 1.2 to 1.3 and E
= 1.6 to 1.8 eV. Figure 5 includes results for the different starting conditions
for H2 in different vibrational (v = 0, 1,...) and rotational
states (j = 0, 1,...). The most impressive feature is that for H2
(v = 0, j = 1) the reaction probability increases steeply
up to 95% with some small resonance features around
E 1.3 eV. The influence of initial rotational excitation has been experimentally
investigated only in the case of inelastic scattering.
1.3 eV. The influence of initial rotational excitation has been experimentally
investigated only in the case of inelastic scattering.
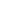 t
has to be shorter than 10 [au]). This smoothing behavior is especially
a result that we have found within our investigations of the Ne + H2+
reaction,55 where we have a much deeper potential minimum leading
to many sharp resonances. The comparison of reactant (RC) and product coordinates
(PC) reveals that if one is interested just in total reaction probabilities
for systems such as H- + H2, calculations with RC
are good enough. The strong difference in reaction probabilities for H2
in different rotational states (v = 0, j = 0, 1, 2,...) reveals
the strong influence of the anisotropy of the PES on the dynamics. For
initial vibrational states v = 2, 3, 4, further total reaction probabilities
are given in Figures 6 and 7.
t
has to be shorter than 10 [au]). This smoothing behavior is especially
a result that we have found within our investigations of the Ne + H2+
reaction,55 where we have a much deeper potential minimum leading
to many sharp resonances. The comparison of reactant (RC) and product coordinates
(PC) reveals that if one is interested just in total reaction probabilities
for systems such as H- + H2, calculations with RC
are good enough. The strong difference in reaction probabilities for H2
in different rotational states (v = 0, j = 0, 1, 2,...) reveals
the strong influence of the anisotropy of the PES on the dynamics. For
initial vibrational states v = 2, 3, 4, further total reaction probabilities
are given in Figures 6 and 7.
 (rhomax) in the time-independent calculations (abc) is chosen large enough
(i.e., compare rhomax = 12 and 15 a0), then the comparison
with "S-F: PC, Rmax = 19.5, Etrans
= 1 eV" is nearly perfect. The resonance structure in the time-independent
calculation (abc) is a little bit different from the WP results, but this
comes from the less dense energy grid in case of the abc calculation. In
addition, one can see that with initial Etrans = 2 eV
we can get reasonable results in one run up to the dissociation energy
of H2. In case of initial Etrans = 1 eV, values
only up to E = 3.5 eV are acceptable. At the moment, it is not clear
why we have a "constant" shift between the results calculated with Etrans
= 1 and 2 eV for Rmax = 17.5a0.
(rhomax) in the time-independent calculations (abc) is chosen large enough
(i.e., compare rhomax = 12 and 15 a0), then the comparison
with "S-F: PC, Rmax = 19.5, Etrans
= 1 eV" is nearly perfect. The resonance structure in the time-independent
calculation (abc) is a little bit different from the WP results, but this
comes from the less dense energy grid in case of the abc calculation. In
addition, one can see that with initial Etrans = 2 eV
we can get reasonable results in one run up to the dissociation energy
of H2. In case of initial Etrans = 1 eV, values
only up to E = 3.5 eV are acceptable. At the moment, it is not clear
why we have a "constant" shift between the results calculated with Etrans
= 1 and 2 eV for Rmax = 17.5a0.
 20 summation
are presented. In a forthcoming paper we will present results where integral
and differential cross sections are derived explicitly from calculations
for total angular momentum J
20 summation
are presented. In a forthcoming paper we will present results where integral
and differential cross sections are derived explicitly from calculations
for total angular momentum J 0.
0.
IV. Summary
Theoretical investigations are performed for the dynamics of reactive scattering
processes using time-dependent wave packet calculations. The system of
interest is the ion-neutral reaction [H + H2]- with
different isotope variants, where the results for the deuterated systems
will be presented in a forthcoming paper. The potentials used in the present
calculations (ab initio and model type) exhibit long-range interactions.
The state-to-state analysis can be performed in reactant or product Jacobi
coordinates.
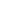 t < 10 [au] and is not
reliable for long propagations, as are needed in the case of deep potentials.
In addition there are problems in handling eq 25 optimally for
R
t < 10 [au] and is not
reliable for long propagations, as are needed in the case of deep potentials.
In addition there are problems in handling eq 25 optimally for
R 0. The efficiency of the wave packet approach compared to the time-independent
hyperspherical approach of Manolopoulos et al.54 has not been
analyzed in detail, but in case a fine energy grid for the reaction probability
was needed, the time-independent approach was more time-consuming (but
on the other hand the full S-matrix was calculated).
0. The efficiency of the wave packet approach compared to the time-independent
hyperspherical approach of Manolopoulos et al.54 has not been
analyzed in detail, but in case a fine energy grid for the reaction probability
was needed, the time-independent approach was more time-consuming (but
on the other hand the full S-matrix was calculated).
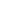 Ecoll
> 1 eV). The present disadvantage is that, in the case of deep potential
energy minima, WP calculations can become very CPU intensive, because the
wave packet is trapped. Applications of wave packet calculations are performed
now on an IBM-SP2 using parallel architecture. Work of optimizing the "parallel"
code is in progress and will be published soon.
Ecoll
> 1 eV). The present disadvantage is that, in the case of deep potential
energy minima, WP calculations can become very CPU intensive, because the
wave packet is trapped. Applications of wave packet calculations are performed
now on an IBM-SP2 using parallel architecture. Work of optimizing the "parallel"
code is in progress and will be published soon.
Acknowledgment
The authors thank G. Balint-Kurti, C. Cerjan, G. Kroes, C. Morari, and
V. Staemmler for support and discussions; especially the help of S. Gray,
for making his real wave packet code available for comparison, is gratefully
acknowledged. We are thankful to A. K. Belayev and W. Meyer for providing
us with the PES code. This work was supported in part by the Deutsche Forschungsgemeinschaft
within the Schwerpunktprogramm "Zeitabhängige Phänomene und Methoden
in Physik und Chemie". The computations have been performed on IBM-RS6000
workstations and on the IBM-SP2 at the Computercenter of the University
of Karlsruhe (SSC). We thank SSC for computer time.
 Part of the special issue "William H. Miller
Festschrift".
Part of the special issue "William H. Miller
Festschrift".
NR, Nr, N

128, 128, 80
number of grid points for product Jacobi coordinates (PC)
NR, Nr, N

128, 64, 32
number of grid points for reactant Jacobi coordinates (RC)
Rmin, Rmax[a0]
0.001, 15.5-19.5
extension of the grid in R in PC and in RC
rmin, rmax[a0]
0.001, 15.5-19.5(g)
extension of the grid in
r in PC (in RC for flux)
Etrans [eV]
0.7, 1.0, 2.0
translation energy
R0
10.0, 12.0
initial location of the center of the WP
 0
00.4
initial width of the WP
Ncheb
6700
number of Chebychev iterations
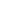 t, T[au]
t, T[au] 10-20, 15000
timings for split operator propagation
A,
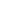 (r, R)abs
(r, R)abs0.015, 4.0
parameters for the absorbing potential (eq 18)










 j')
+ H- (SM potential): state-to-state reaction probabilities (in
PCs) for different rotationally summed vibrational product states (Rmax
= 17.5 a0, Etrans = 1.0 eV).
j')
+ H- (SM potential): state-to-state reaction probabilities (in
PCs) for different rotationally summed vibrational product states (Rmax
= 17.5 a0, Etrans = 1.0 eV).


